|
Математические головоломки, логические задачи, игры
|
|
|
« Татьяна »
|
Дата: Воскресенье, 19 Июня 2011, 01:06:19 | Сообщение # 1
|
|
Любознательные
|
Сообщений: 188
|
|
|
 
Математика "для всех времен и народов"
Не удивительно, что занимательная математика стала развлечением «для всех времен и народов». Уже в папирусе Ринда – Ахмеса, который датируется XX в. до н. э., среди 84 задач, которые сейчас можно было бы отнести к прикладной математике, встречаются и задачи занимательного характера, варианты которых в течение последующих тысячелетий кочевали из одного сборника задач по занимательной математике в другой. Несмотря на существование тринадцатитомных «Начал» Евклида (III в. до н. э.), ставших более чем на два тысячелетия образцом научной строгости, и в Древней Греции занимательный элемент в математике не исчез и наиболее ярко представлен в «Арифметике» Диофанта Александрийского (вероятно, III в.). В Средние века самый глубокий след в занимательной математике оставили итальянцы Леонардо (Фибоначчи) из Пизы (XIII в.) и Никколо Тарталья (XVI в.).
Сборники математических развлечений, похожие на современные, начали появляться с XVII в. Среди них особой популярностью пользовались «Приятные и занимательные задачи, рассматриваемые в числах» математика и поэта Гаспара Клода Баше сьер де Мезириака и «Математические и физические развлечения» другого французского математика и писателя Жака Озанама.
Все возможно...
Сообщение отредактировал(а) Татьяна - Воскресенье, 19 Июня 2011, 01:43:03
|
|
|
|
|
|
« Татьяна »
|
Дата: Воскресенье, 19 Июня 2011, 01:16:38 | Сообщение # 2
|
|
Любознательные
|
|
Сообщений: 188
|
|
|
Детская математичская шутка (на извлечение корня) Как доказать, что 2*2= 5!!! 
2*2=5
16-36=25-45
16-36+201/4=25-45+201/4
42-2*4*9/2+(9/2)2 = 52-2*5*9/2+(9/2)2
(4-(9/2)2)=(5-(9/2)2)
4-9/2=5-9/2
4=5
2*2=5
решение для нежелающих мозг хоть немного поднапрячь ...
Выделяйте и читайте...
ошибка состоит в заключении...
(4-(9/2)2)=(5-(9/2)2)
4-9/2=5-9/2
т.к. квадрат и положительного и отрицательного чисел равны, но сами положительное и отрицательное числа нет...
Все возможно...
Сообщение отредактировал(а) Татьяна - Воскресенье, 19 Июня 2011, 01:18:46
|
|
|
|
|
|
« Татьяна »
|
Дата: Воскресенье, 19 Июня 2011, 01:28:34 | Сообщение # 3
|
|
Любознательные
|
|
Сообщений: 188
|
|
|
Чему равно 84, если 8*8=54?
Чем отличается программист от нормального человека?
Нормальный человек думает, что в килобайте 1000 байт,
программист же думает, что в километре 1024 метра.
(подсказка)
решение.
Вопрос вовсе не странный, если учесть , что мы можем применять и не десятичную систему счисления... (позиционную)
Для примера в вычислительной технике используется двоичная (с основанием числа 2) и частенько 16-ричная (с основанием 16)0-9,a,b,c,d,e,f ...
Пусть основание незвестной системы равно Х.
Число 84 тогда означает 8 единиц второго разряда и 4 единицы первого порядка
84=8*х+4
Число 54 обозначает 5*х+4
8*8=5х+4
те.е в десятичной системе счисления 64=5х+4,
откуда х=12
Числа написаны в 12-ричной системе и
"84"=8*12+4=100
Все возможно...
Сообщение отредактировал(а) Татьяна - Воскресенье, 19 Июня 2011, 02:04:44
|
|
|
|
|
|
« Татьяна »
|
Дата: Воскресенье, 19 Июня 2011, 02:17:51 | Сообщение # 4
|
|
Любознательные
|
|
Сообщений: 188
|
|
|
Жизнь Диофанта
История сохранила нам мало черт биографии замечательного древнего математика Диофанта. Все, что известно о нем, почерпнуто из надписи на его гробнице — надписи, составленной в форме математической задачи. Мы приведем эту запись.
На родном языке
На языке алгебры
[table][tr][td]Путник! Здесь прах погребен
Диофанта. И числа поведать
Могут, о чудо, сколь долог
был век его жизни.[/td][td]x[/td][/tr][tr][td]
Часть шестую его представляло
прекрасное детство. [/td][td]х/6[/td][/tr][tr][td]Двенадцатая часть протекла
еще жизни — покрылся
Пухом тогда подбородок.[/td][td]х/12[/td][/tr][tr][td]Седьмую в бездетном
Браке провел Диофант. [/td][td]х/7[/td][/tr][tr][td]Прошло пятилетие; он
Был осчастливлен рожденьем
прекрасного первенца сына,[/td][td]5[/td][/tr][tr][td]
Коему рок половину лишь
жизни прекрасной и светлой
Дал на земле по сравненью с отцом. [/td][td]х/2[/td][/tr][tr][td]И в печали глубокой
Старец земного удела конец
восприял, переживши
Года четыре с тех пор, как
сына лишился. [/td][td]х=х/6+х/12+х/7+5+х/2+4[/td][/tr][/table]
Скажи, сколько лет жизни достигнув,
Смерть восприял Диофант?
Решение.
Решив уравнение и найдя, что x = 84, узнаем следующие черты биографии Диофанта: он женился в 21 год, стал отцом на 38 году, потерял сына на 80-м году и умер в возрасте 84 года.
Все возможно...
|
|
|
|
|
|
« Татьяна »
|
Дата: Воскресенье, 19 Июня 2011, 03:04:07 | Сообщение # 5
|
|
Любознательные
|
|
Сообщений: 188
|
|
|
Логическая задачка...
Парадокс лжеца
По преданию, Эпименид утверждал, что все критяне лжецы. Верно ли это утверждение, если учесть, что сам Эпименид родом с острова Крит?
Эпименид — легендарный греческий поэт, живший на Крите в VI в. до н. э. Приписываемое ему утверждение логически противоречиво, если предположить, что лжецы всегда лгут, а нелжецы всегда говорят правду. При таком предположении утверждение «Все критяне лжецы» не может быть истинным, ибо тогда Эпименид был бы лжецом и, следовательно, то, что он утверждает, было бы ложью. Но приписываемое Эпимениду утверждение не может быть и ложным, ибо это означало бы, что критяне говорят только правду и, следовательно, то, что сказал Эпименид, также истинно.
Древних греков очень занимало, каким образом, казалось бы, вполне осмысленное утверждение не может быть ни истинным, ни ложным без того, чтобы при этом не возникло противоречия. Философ-стоик Хризипп написал шесть трактатов о парадоксе лжеца, ни один из которых не сохранился до нашего времени. Парадокс лжеца преждевременно свел в могилу греческого поэта Филета Косского, который был настолько тощ, что, по преданию, подкладывал в сандалии свинец, чтобы его не унес ветер.
В Новом Завете апостол Павел повторяет парадокс лжеца в послании к Титу (гл. I стих 12—13):
Из них же самих один стихотворец сказал: «Критяне
всегда лжецы, злые звери, утробы ленивые».
Свидетельство это справедливо...
Неизвестно, знал ли апостол Павел о парадоксе, содержащемся в этих утверждениях.
Почему эта форма парадокса лжеца, в которой утверждение сообщает нам нечто о себе, отличается большей ясностью? Потому, что она исключает всякую неоднозначность по поводу того, всегда ли лжец лжет, а говорящий правду изрекает истину.
Существует бесчисленное множество вариантов парадокса лжеца. Бертран Рассел утверждал, что, по его мнению, философ Джордж Эдвард Мур солгал единственный раз в жизни: когда кто-то спросил Мура, всегда ли он говорит правду, Мур, подумав, ответил: «Нет».
Мы столкнулись с известным парадоксом лжеца. Простейший вариант — утверждение, гласящее: «Это утверждение ложно». Истинно ли оно? Если оно истинно, то оно ложно! Ложно ли оно? Если оно ложно, то оно истинно! Такого рода противоречивые утверждения встречаются гораздо чаще, чем вы думаете.
По материалам «А ну-ка, догадайся!». Мартин Гарднер.
Все возможно...
Сообщение отредактировал(а) Татьяна - Воскресенье, 19 Июня 2011, 03:04:54
|
|
|
|
|
|
« Татьяна »
|
Дата: Воскресенье, 19 Июня 2011, 03:13:34 | Сообщение # 6
|
|
Любознательные
|
|
Сообщений: 188
|
|
|
Легенда арабского писателя Асафада
Существует легенда, индусского происхождения, которую рассказывает арабский писатель Асафад.
Брамин Сесса, сын Дагера, придумал игру в шахматы, где король, хотя и самая важная фигура, не может ступить шагу без помощи и защиты своих подданных пешек и других фигур. Изобрел он эту игру в забаву своему монарху и повелителю Индии, Шерану. Царь Шеран, восхищенный выдумкой брамина, сказал, что даст ему все, что только брамин захочет.
— В таком случае, — сказал Сесса, — прикажи дать мне столько пшеничных зерен, сколько их получится, если на первую клетку шахматной доски положить зерно, на вторую 2, на третью 4, на четвертую 8 и т. д., все удваивая, пока не дойдут до 64-й клетки.
Повелитель Индии не смог этого сделать. Число требуемых зерен выражалось двадцатизначным числом. Чтобы удовлетворить «скромное» желание брамина, нужно было бы восемь раз засеять всю поверхность земного шара и восемь раз собрать жатву. Тогда бы только получилось нужное для Сессы количество зерен.
Обещать «все, что хочешь», легко, но трудно исполнить!
Желающие могут привести и саму прогрессию...
Все возможно...
|
|
|
|
|
|
« Татьяна »
|
Дата: Воскресенье, 19 Июня 2011, 03:18:06 | Сообщение # 7
|
|
Любознательные
|
|
Сообщений: 188
|
|
|
Древнеиндийская легенда о конце мира
Легенда эта гласит, будто в городе Бенаресе, под куполом главного храма, в том месте, где находится середина Земли, бог Брама поставил вертикально на бронзовой площадке три алмазные палочки, каждая длиною в локоть и толщиною в корпус пчелы.
При сотворении мира на одну из этих палочек были надеты 64 кружка из чистого золота с отверстиями посередине — так, что они образовали род усеченного конуса, так как диаметры их шли в возрастающем порядке, начиная сверху.
Жрецы, сменяемые один другим, днем и ночью без устали трудятся над перенесением этой колонны кружков с первой палочки на третью, пользуясь второй как вспомогательной, причем они обязаны соблюдать уже указанные условия, т.е. не переносить за один раз более одного кружка и класть снятый кружок или на свободную в этот момент палочку, или накладывать его на кружок только большего диаметра. Когда, соблюдая все эти условия, жрецы перенесут все 64 кружка с первой палочки на третью, наступит конец мира...
Допустим, что перенос одного кружка продолжается всего одну секунду, тогда на перемещение пирамиды из восьми кружков потребуется чуть больше 4 минут. Что же касается переноса башни в 64 кружков, то на это понадобится
18 446 744 073 709 551 615 сек.
А это значит, ни более и ни менее, как пять с лишним миллиардов веков.
PS. Посему Конец Света еще пока не предвидится... Живем дальше...
Все возможно...
Сообщение отредактировал(а) Татьяна - Воскресенье, 19 Июня 2011, 03:19:07
|
|
|
|
|
|
« Tarki »
|
Дата: Понедельник, 20 Июня 2011, 22:18:12 | Сообщение # 8
|
|
Любопытные
|
Сообщений: 46
|
|
|
Quote ( Татьяна @ Вчера, 03:13:34)  ) Желающие могут привести и саму прогрессию...
Зачем проделывать то чтоне удалось царю. У меня нет столько пшена сколько было у царя
|
|
|
|
|
|
« Татьяна »
|
Дата: Суббота, 25 Июня 2011, 01:34:18 | Сообщение # 9
|
|
Любознательные
|
|
Сообщений: 188
|
|
|
Треугольник Паскаля  .
геометрическая форма  .
в цифрах... 
Треугольник Паскаля — арифметический треугольник, образованный биномиальными коэффициентами. Назван в честь Блеза Паскаля.
Если очертить треугольник Паскаля, то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух, расположенных над ним чисел. Продолжать треугольник можно бесконечно. Строки треугольника симметричны относительно вертикальной оси. Имеет применение в теории вероятности и обладает занимательными свойствами.
Первое упоминание треугольной последовательности биномиальных коэффициентов под названием meru-prastaara встречается в комментарии индийского математика X века Халаюдхи к трудам другого математика, Пингалы. Треугольник исследуется также Омаром Хайямом около 1100 года, поэтому в Иране эту схему называют треугольником Хайяма. В 1303 году была выпущена книга «Яшмовое зеркало четырёх элементов» китайского математика Чжу Шицзе, в которой был изображен треугольник Паскаля на одной из иллюстраций; считается, что изобрёл его другой китайский математик, Ян Хуэй (поэтому китайцы называют его треугольником Яна Хуэя).
Свойства
* Второе число каждой строки соответствует её номеру.
* Третье число каждой строки равно сумме номеров строк, ей предшествующих.
* Третье число каждой строки является треугольным.
* Четвертое число каждой строки является тетраэдрическим.
* Сумма чисел n-й восходящей диагонали, проведенной через строку треугольника с номером n − 1, есть n-е число Фибоначчи
* Если вычесть из центрального числа в строке с чётным номером соседнее число из той же строки, то получится число Каталана
* Сумма чисел n-й строки треугольника Паскаля равна 2n (при счёте номеров строк, начиная с нуля).
* Простые делители чисел треугольника Паскаля образуют симметричные самоподобные структуры.
* Если в треугольнике Паскаля все нечётные числа окрасить в чёрный цвет, а чётные - в белый, то образуется треугольник Серпинского.
* Все числа в n-й строке кроме единиц делятся на число n, если и только если n является простым числом.(следствие теоремы Люка)
* Если сложить все числа с порядковым номером вида 3n, 3n+1, 3n+2 в строке с нечетным номером, то первые две суммы будут равны, а третья на 1 меньше.
А еще проще объясняют устройство треугольника Паскаля слова: каждое число равно сумме двух расположенных над ним чисел. Все элементарно, но сколько в этом таится чудес.
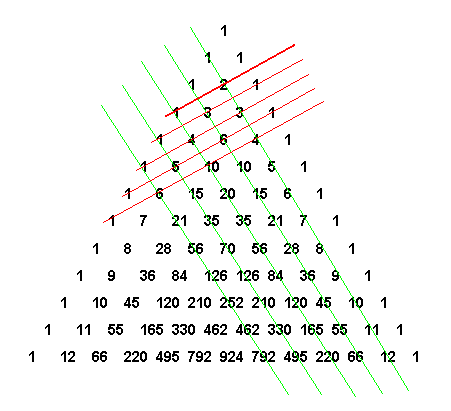
На вершине треугольника стоит 1. Треугольник можно продолжать неограниченно. Он обладает симметрией относительно вертикальной оси, проходящей через его вершину. Вдоль диагоналей (насколько у треугольника могут быть диагонали, но не будем придираться, такая терминология встречается в публикациях), параллельных сторонам треугольника (на рисунке отмечены зелеными линиями) выстроены треугольные числа и их обобщения на случай пространств всех размерностей.
Треугольные числа в самом обычном и привычном нам виде показывают, сколько касающихся кружков можно расположить в виде треугольника - как классический пример начальная расстановка шаров в бильярде. К одной монетке можно прислонить еще две - итого три - к двум можно приладить еще три - итого шесть. Продолжая наращивать ряды с сохранением формы треугольника получим ряд 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66..., что и показывает вторая зеленая линия. Этот замечательный ряд, каждый член которого равен сумме натурального ряда чисел (55=1+2+3+4+5+6+7+8+9+10), содержит также множество знакомцев, хорошо известных любителям математики: 6 и 28 - совершенные числа, 36 - квадратное число, 8 и 21 - числа Фибоначчи.
Следующая зеленая линия покажет нам тетраэдральные числа - один шар мы можем положить на три - итого четыре, под три подложим шесть (напрягитесь и представьте!) - итого десять, и так далее. 
А следующая зеленая линия (1, 5, 15, 35,...) продемонстрирует попытку выкладывания гипертетраэдра в четырехмерном пространстве - один шар касается четырех, а те, в свою очередь, десяти... В нашем мире такое невозможно, только в четырехмерном, виртуальном. И тем более пятимерный тетраэдр, о котором свидетельствует следующая зеленая линия, он может существовать только в рассуждениях топологов.
А о чем же говорит нам самая верхняя зеленая линия, на которой расположились числа натурального ряда? Это тоже треугольные числа, но одномерные, показывающие, сколько шаров можно выложить вдоль линии - сколько есть, столько и выложите. Если уж идти до конца, то самый верхний ряд из единиц - это тоже треугольные числа в нульмерном пространстве - сколько бы шаров мы не взяли - больше одного расположить не сможем, ибо просто негде - нет ни длины, ни ширины, ни высоты.
Даже беглого взгляда, брошенного на треугольник Паскаля, достаточно, чтобы отметить следующие любопытные факты: 10 ядер можно сложить и в виде тетраэдра и в виде плоского треугольника. А 56 гиперядер, образующих тетраэдр в пятимерном пространстве, можно уложить в обычный привычный трехмерный тетраэдр, однако, если бы мы попытались выложить из 56 ядер треугольник, то одно ядро осталось бы лишним.
Суммы чисел, стоящих вдоль не столь круто падающих диагоналей (на рисунке отмечены красными линиями) образуют хорошо известную последовательность Фибоначчи. Числа Фибоначчи часто встречаются и в комбинаторных задачах. Рассмотрим ряд из n стульев. Сколькими способами можно рассадить на них мужчин и женщин так, чтобы никакие две женщины не сидели рядом? При n=1, 2, 3, 4, ... число способов соответственно равно 2, 3, 5, 8, ..., то есть совпадает с числами Фибоначчи. Паскаль, по-видимому, не знал, что числа Фибоначчи скрыты в его треугольнике. Это обстоятельство было обнаружено только в XIX веке. Числа, стоящие на горизонтальных строках треугольника Паскаля, - это биномиальные коэффициенты, то есть коэффициенты разложения (x+y)n по степеням x и y. Например, (x+y)2=x2+2xy+y2 и (x+y)3=x3+3x2y+3xy2+y3. Коэффициенты разложения 1, 2, 2 стоят во второй строке, а 1, 3, 3, 1 - в третьей строке треугольника. Чтобы найти коэффициенты разложения (x+y)n, достаточно взглянуть на n-ую строку треугольника. Именно это фундаментальное свойство треугольника Паскаля связывает его с комбинаторикой и теорией вероятности, превращая в удобное средство проведения вычислений.
Предположим (пример от Мартина Гарднера), что некий шейх, следуя законам гостеприимства, решает отдать вам трех из семи своих жен.  Сколько различных выборов вы можете сделать среди прекрасных обитательниц гарема? Для ответа на этот волнующий вопрос необходимо лишь найти число, стоящее на пересечении диагонали 3 и строки 7: оно оказывается равным 35. Если, охваченные радостным волнением, вы перепутаете номера диагонали и строки и будете искать число, стоящее на пересечении диагонали 7 со строкой 3, то обнаружите, что они не пересекаются. То есть сам метод не дает вам ошибиться!
Все возможно...
Сообщение отредактировал(а) Татьяна - Суббота, 25 Июня 2011, 02:31:21
|
|
|
|
|
|
Новости
Блог
Статьи
Фото
Видео
Муз
Игры
ТВ
Радио
Форум
Чат
CSS
К-сайта
FAQ
E
Tagis 
. 
